On-going Projects

My current research at UCF is concentrated on the spectral theory of certain nonlinear integrable PDEs (fNLS and KdV in particular). It is well-known that solitons and breathers (two types of special solutions) represent localized solutions to many integrable system. We are interested in studying the statistical ensembles of solitons/breathers, which are so-called soliton/breather gases. The study of soliton/breather gases provides a possibility to understand one of the most intriguing phenomena of modern science - turbulence in dynamical systems[see Za2009].
In one project, we consider fNLS soliton/breather gas. We derive average densities and fluxes for such gases by studying the thermodynamic limit of the fNLS finite gap solutions. One of the central objects in the spectral theory of soliton/breather gases is the nonlinear dispersion relation integral equation (NDR): $\begin{align*} \int_{\Gamma^+} \left[\log\left| \frac{w-\bar z}{w-z}\right|+ {\log\left|\frac{R_0(z)R_0(w)+z w -\delta_0^2} {R_0(\bar z)R_0(w)+\bar z w-\delta_0^2}\right|}\right] u(w) d\lambda(w) +\sigma(z)u(z) &= \Im R_0(z), \\ \int_{\Gamma^+} \left[\log\left| \frac{w-\bar z}{w-z}\right|+{\log\left|\frac{R_0(z)R_0(w)+ z w-\delta_0^2} {R_0(\bar z)R_0(w)+ \bar z w-\delta_0^2}\right|}\right] v(w) d\lambda(w) +\sigma(z)v(z) &= - 2\Im[z R_0(z)], \end{align*}$

where $R_0(z)=\sqrt{z^2-\delta_0^2}$ with the branchcut $\gamma_0=[-\delta_0,\delta_0]\subset i\mathbb{R}$ being the exceptional (permanent) band, $\Gamma^+\subset \mathbb{C}^+\setminus \gamma_0$ is a compact, $z\in\Gamma^+$, $\sigma$ is a continuous non negative function on $\Gamma^+$ and $\lambda$ is some reference measure (arclength measure if $\Gamma^+$ is a contour, area measure if $\Gamma^+$ is a 2D region) on $\Gamma^+$ that reflects the density of accumulating in the thermodynamic limit bands. In the case of $\delta_0=0$ the fNLS breather gas reduces to the fNLS soliton gas with the NDR given by removing the blue parts in the breather NDR. The solution $u(z)$ to the first NDR (assuming the existence) is called density of states, which plays a fundamental role in our project. With the help of finite-gap theory, we established the following results:

Computing the averaged conserved quantities (i.e., the densities and fluxes) under thermodynamic limit. For example, in the soliton gas case, the averaged densities can be computed by the following elegant formula:
$\begin{align*} I_m =2\int_{\Gamma^+}u(\zeta)\Im \zeta^m d\lambda(\zeta), \end{align*}$
where $u$ is the density of states, and $I_m$ denotes the averaged density that is associate with the coefficient of the expansion of quasimomentum differential:
$\begin{align*} dp=\left(1-\sum_{m=1}^\infty\frac{I_m}{z^{m+1}}\right)dz. \end{align*}$
In the paper [TW2022], we present the formulae of computing averaged densities for fNLS breather gases. The results provide certain statistical properties of the soliton/breather ensembles.
Motivated by some formal WKB analysis results on the periodic Zakharov-Shabat operator, we solve the first NDR equation explicitly in both breather and soliton gas limit cases. We call them periodic gases. In the periodic gases case, the density of state is represented by the following formula:
$u(z)= \frac{| z|}{\pi L}\int_{0}^{q^{-1}(| z|)}\frac{dx} {\sqrt{q^2(x)+ z^2}},\quad z\in\Gamma^+,$
where $q(x)$ is some periodic function as the potential in the Zakharov-Shabat operator. One surprising result is that $u$ is proportional to the density function of the centers of the bands (the spectra of the periodic Zakharov-Shabat operator).
We established some fundamental error estimates in the thermodynamic-type limit. Specifically speaking, we give the large N leading behavior of certain differentials defined on the genus 2N Riemann surface. And those error estimates provide a rigorous mathematical foundation of deriving the NDR equations as well as of computing the averaged conserved quantities. Our results constitute another step towards the mathematical foundation for the spectral theory of fNLS soliton and breather gases that appeared in work of G. El and A. Tovbis\cite{ET2020}.[This project is joint work with Alexander Tovbis.]

Past Projects

The main object of my dissertation research is the AKNS hierarchy:

$\begin{align*} % \label{lax pair AKNS} \psi_x=\begin{pmatrix} iz& p(x,t)\\ q(x,t)& -iz \end{pmatrix}\psi,\quad \psi_t=\sum_{j=1}^nV(p,q)z^j, \end{align*}$

where $\psi(z;x,t)\in GL(2;\mathbb{C};\mathbb{R},\mathbb{R}_+)$. We are mainly interested in studying the long-time ($t\rightarrow\infty$) behaviors of the potential $p(x,t)$ in different sectors of the $(x,t)$ plane. Through Riemann-Hilbert formulations (one modern way of formulating inverse scattering problems), we then apply so-called $\bar\partial$-steepest descent method (a variant of the famous Deift-Zhou’s nonlinear steepest descent method) to derive the explicit asymptotics in three regions (namely, fast decaying region, Painlevé region, fast oscillating region) in the $(x,t)$ plane. And in each region, the error estimates are also provided. In particular, in the Painlevé region, the asymptotic solutions to the mKdV hierarchy (the odd part of AKNS hierarchy) are associated to the Painlevé II hierarchy. The details are presented in this paper by Ma and Myself.

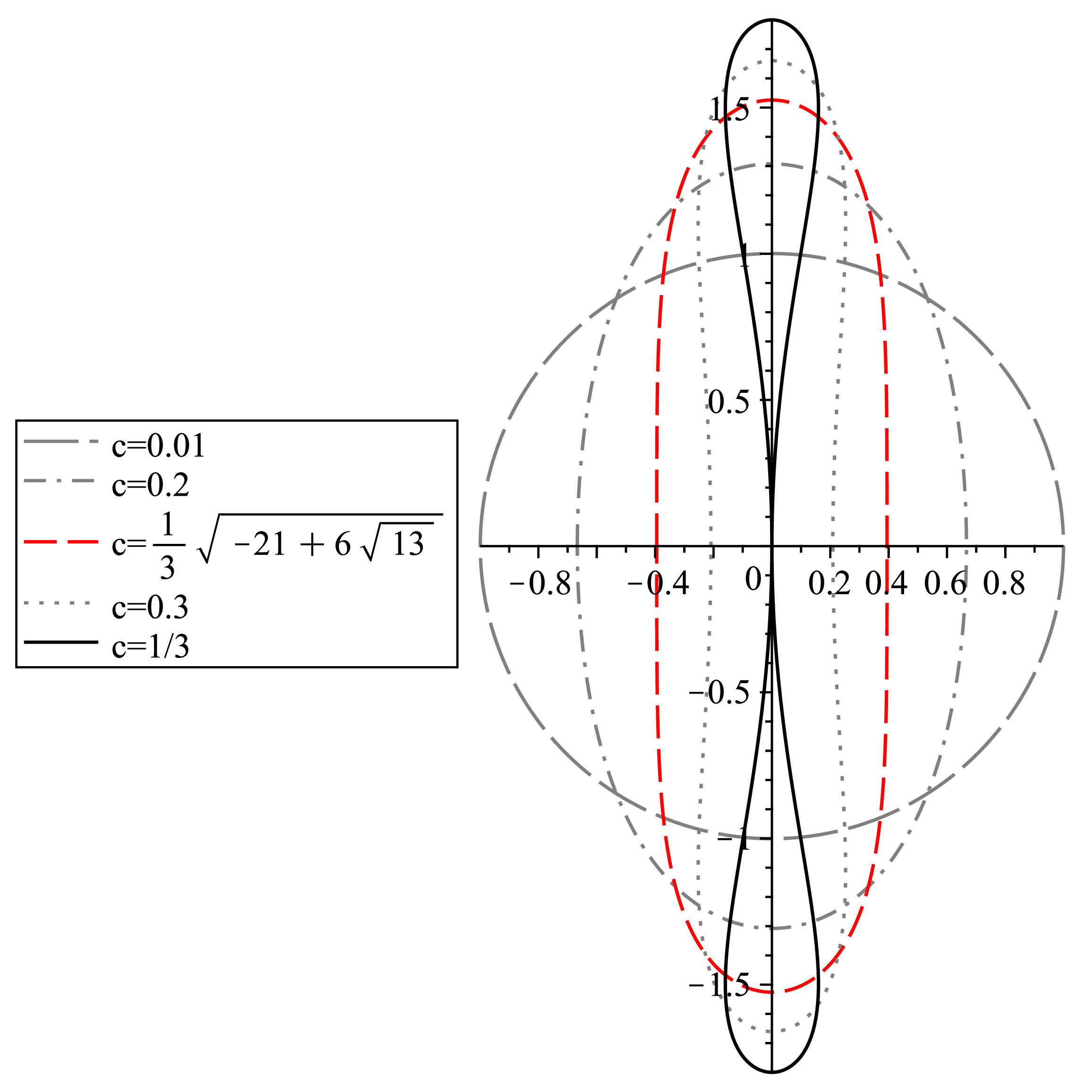
Besides the main project, I also want to mention a side project which emphasizes on complex analysis. Consider a droplet in a electric field (as presented by a complex potential $g$), the equilibrium state of the droplet results in the following free-boundary problem satisfied on the boundary (to be determined):

$\begin{equation*} F(z)=\int^z (g'(s))^2 ds = p \bar{z} + i \tau \dot{\bar{z}}, \end{equation*}$

where “dot” here represents the derivative with respect to arc length, and for positive constants $p$ (representing the strength of the pressure force), $\tau$ (representing the strength of the force due to surface tension). The task is to find solutions to the free boundary problem, i.e., find $z=z(s)$, s is in the unit disc, and $F(z)$ satisfying the stated equation as well as the physical condition that $\sqrt{F’(z)}$ is single-valued. Our result provides a family of solutions (so-called physical droplets, see the Figure in the middle, where a family of physical droplets is presented.). More details are presented in the paper by Hayford and myself.